Centrality Analysis
Centrality analysis is a fundamental concept in social network analysis that helps identify the most important or central nodes within a network.
Degree Centrality
In this enhanced code:
Add a calculate_degree_centrality function to compute the degree centrality for nodes in the social network.
| Calculating Degree Centrality |
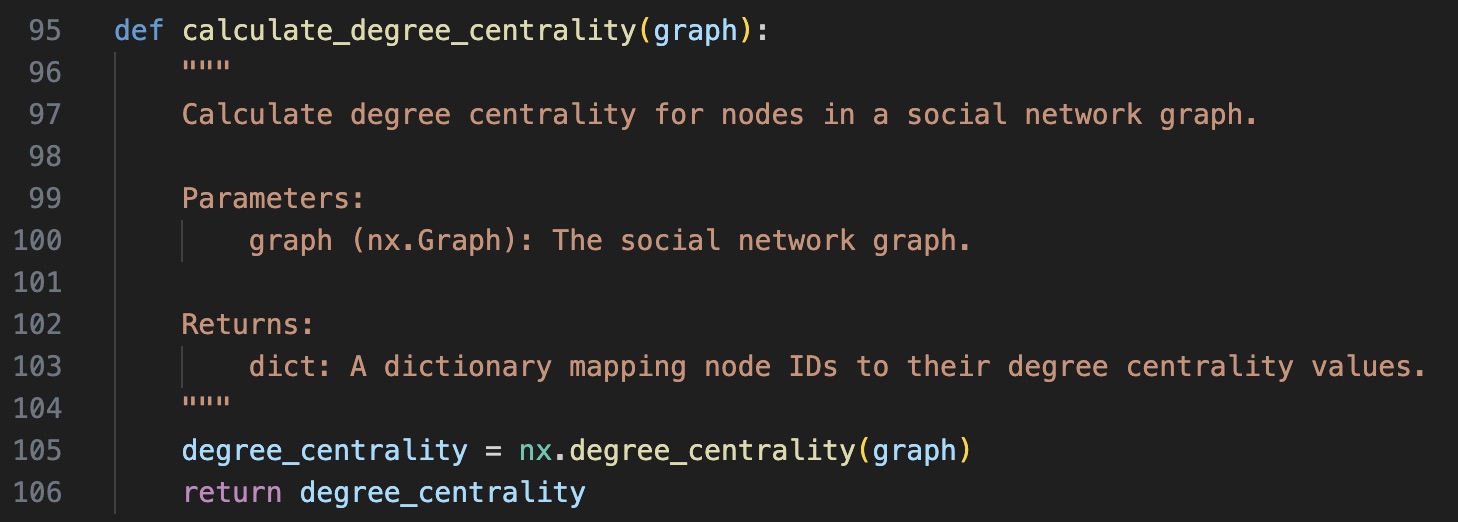 |
After simulating influence propagation, we calculate degree centrality scores for all nodes and visualise the information.
| Visualising Degree Centrality |
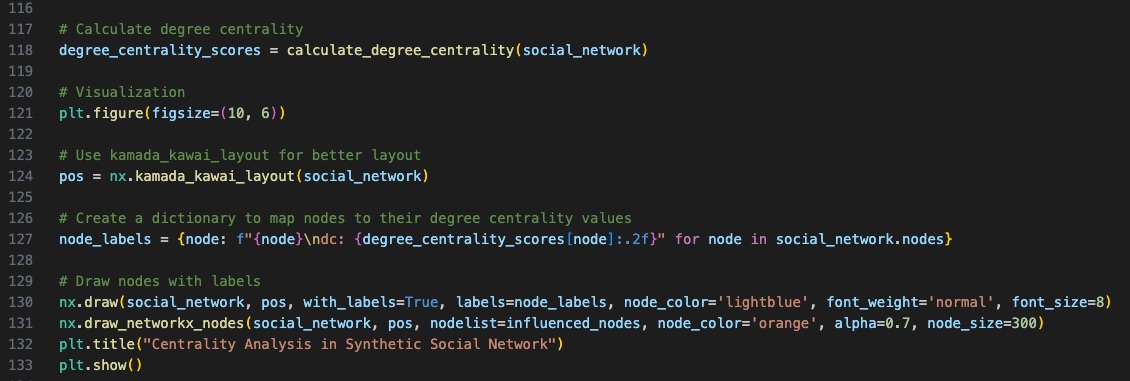 |
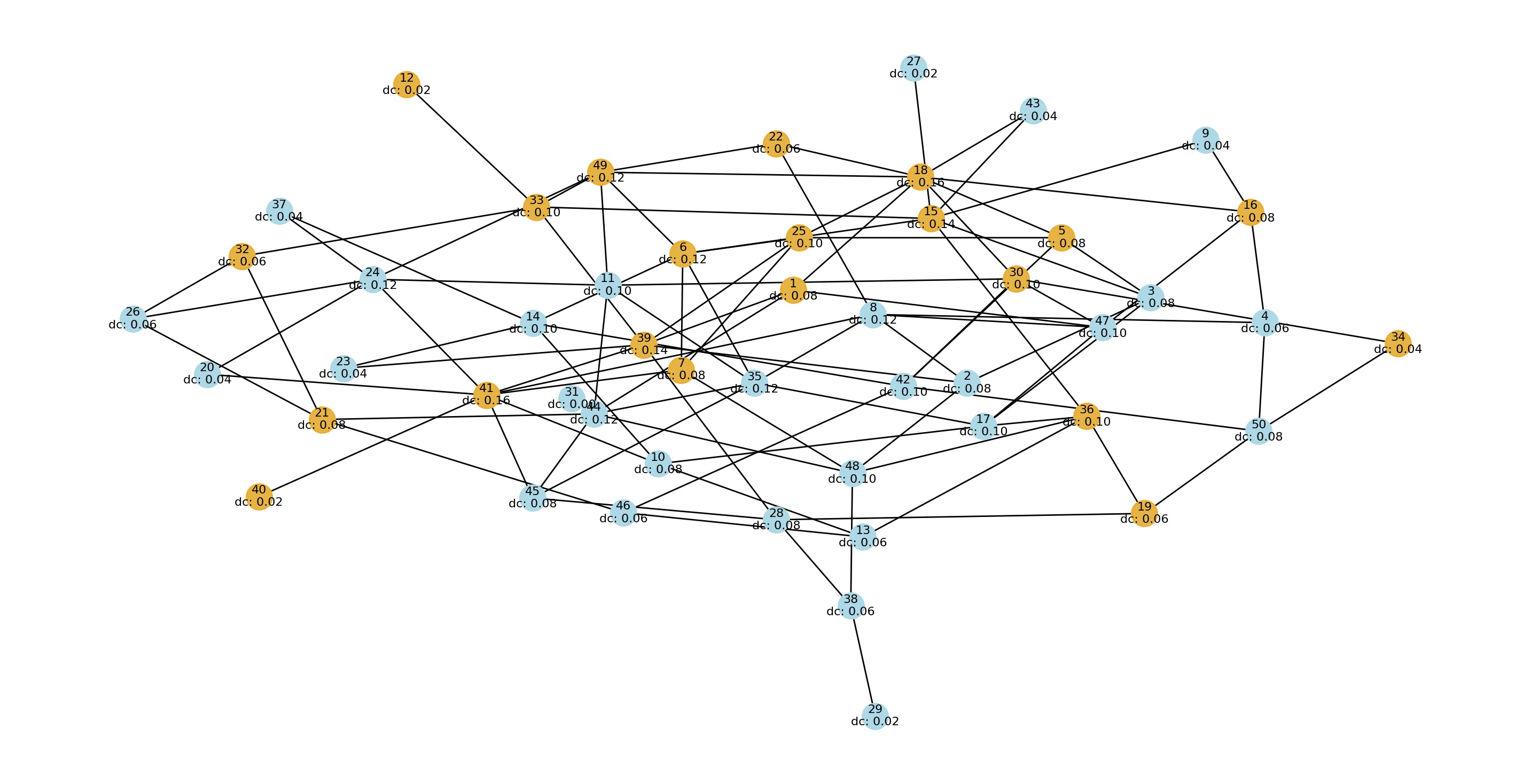 |
Why Degree Centrality?
When examining degree centrality in a social network:
- Identify nodes with many connections.
- Understand which nodes play central roles.
- See who connects different groups.
- Assess potential influence spreaders.
- Analyze network structure.
- Find bridges between communities.
- Evaluate vulnerability points.
- Pinpoint campaign targets.
- Identify key decision-makers.
- Reveal social dynamics.
Is the higher the degree centrality, the better it is?
Higher degree centrality indicates more connections, but whether it's "better" depends on the specific context and objectives of the analysis. In some cases, having many connections may be advantageous, while in others, it might not be desirable.
Advantages:
- Information Spread: High degree centrality can facilitate the spread of information, making it useful for spreading ideas or marketing campaigns.
- Influence: Nodes with many connections can have a substantial influence on the network, which can be advantageous in various scenarios.
- Efficiency: In some networks, high connectivity can lead to more efficient communication and coordination.
Disadvantages:
- Vulnerability: Nodes with high degree centrality are often vulnerable to network disruptions. Targeting them can have a significant impact on the network's function.
- Overload: Nodes with too many connections might become overwhelmed with information or demands, reducing their effectiveness.
- Isolation: Extremely high degree centrality may lead to isolation from specific groups or communities within the network.
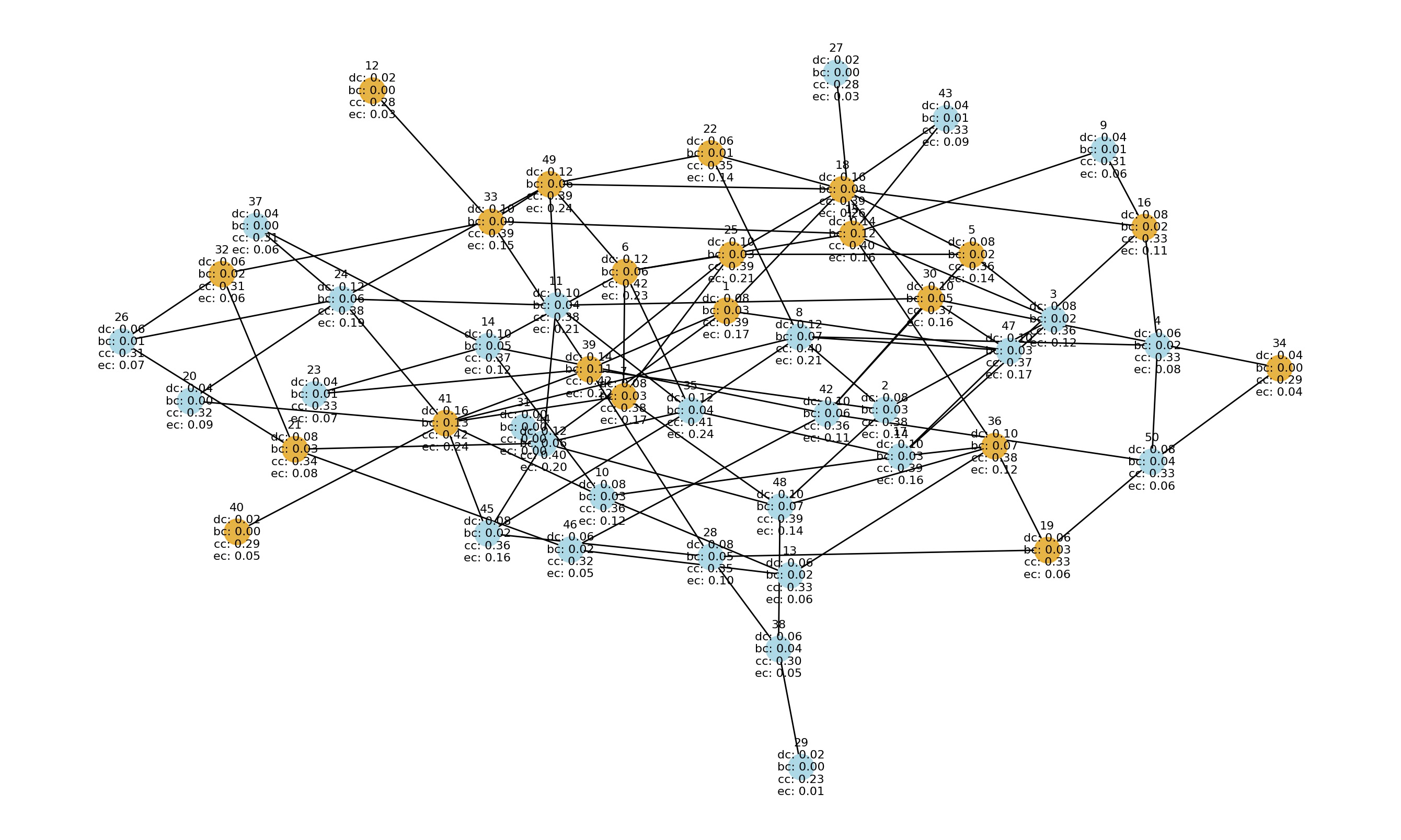
Betweenness Centrality:
Definition: Betweenness centrality measures the extent to which a node lies on the shortest paths between other nodes in the network. It quantifies a node's potential to control or influence the flow of information. Insights: Identifies nodes that act as bridges or critical intermediaries in the network. Useful for finding nodes that can control information flow between different groups or communities. Nodes with high betweenness centrality are crucial for network resilience and fault tolerance.
Closeness Centrality:
Definition: Closeness centrality quantifies how close a node is to all other nodes in the network, considering the length of the shortest paths. It reflects how quickly information can spread from a node to others. Insights: Identifies nodes that can rapidly disseminate information to other nodes in the network. Helps in understanding the efficiency of communication and the accessibility of nodes. Nodes with high closeness centrality are central to fast information diffusion.
Eigenvector Centrality:
Definition: Eigenvector centrality measures a node's centrality based on the centrality of its neighbors. It assigns higher centrality to nodes connected to other central nodes. Insights: Identifies nodes that are well-connected to other central nodes in the network. Reflects a node's influence potential, taking into account the influence of its neighbors. Nodes with high eigenvector centrality are influential because they are connected to influential neighbors.
| Other Centrality Measures |
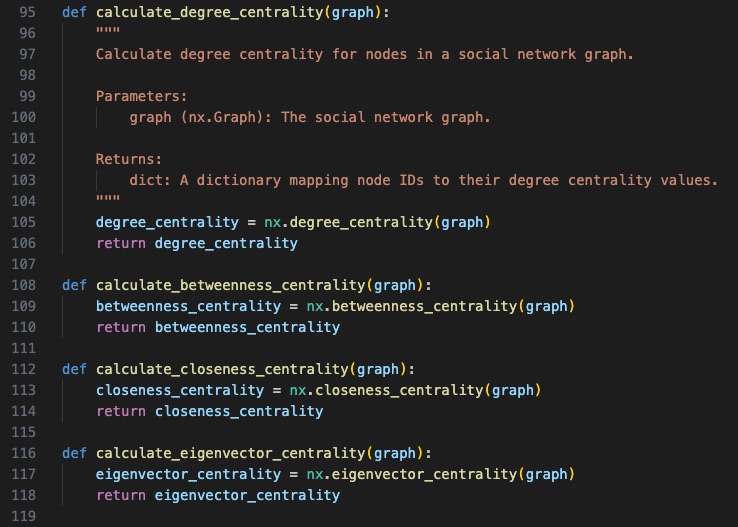 |
 |
 |